I recently learned D way Heap from the following book.
Advanced Algorithms and Data StructuresSo, I tried to implement it in TypeScript. A binary heap is one of D way heap if a parent has two child nodes.
D way heap is a good algorithm if you often need to take the biggest/smallest item from the item list.
If you want to check all the code, go to my repository.
How does Heap look like
Heap can be implemented in an array. Look at the image below. This is Max-Heap. The bigger number is located upper side. A parent has children that have smaller value/priority. The number at the right side of each node is the index of the array.
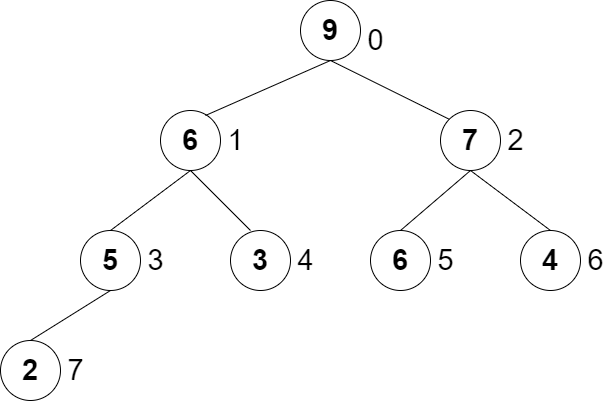
As you can see, the values are not sorted as an array but it’s sorted if you see it as a tree.
If the branching factor is 2, you can calculate a parent node index and child index in the following way.
- A parent : (i – 1)/2
- First child: 2 * i + 1
- Second child: 2 * i + 2
If you are at index 3…
- A parent : (3 – 1)/2 = 1
- First child : 2 * 3 + 1 = 7
- Second child: 2 * 3 + 2 = 8
Insert a new node
When inserting a new node, the new node must always be added to the end of the array. Then, the value needs to be compared with the parent node. If the new node is bigger than the parent, swap the two nodes.
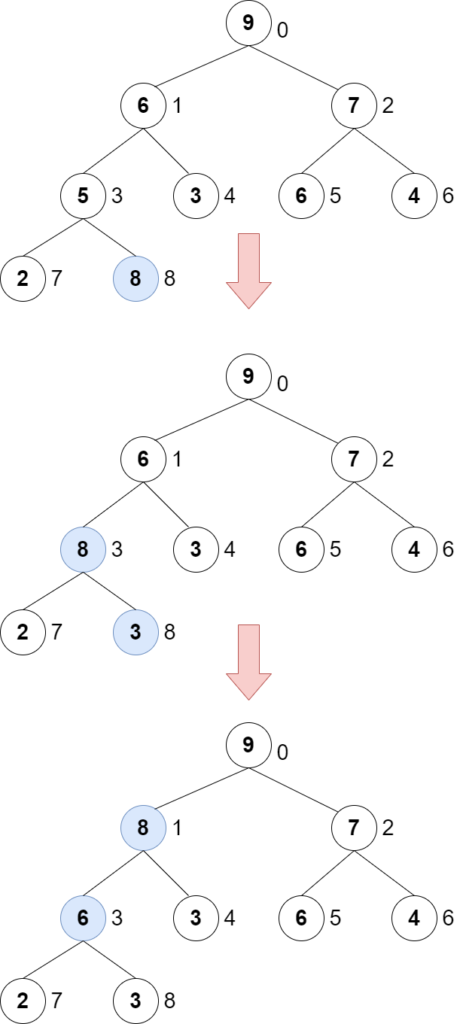
push method inserts a new node, and compares and swaps the nodes.
export abstract class DwayHeapBase<T> {
constructor(
private readonly _branchFactor = DEFAULT_BRANCH_FACTOR,
private elements: T[] = [],
) { }
/**
* Compare the two elements
* @param x
* @param y
* @returns 1 if x > y, -1 if x < y, 0 if x = y
*/
protected abstract compare(x: T, y: T): number;
public get size(): number {
return this.elements.length;
}
public get branchFactor(): number {
return this._branchFactor;
}
public push(element: T): void {
if (element === undefined || element === null || typeof element === "function") {
throw new TypeError("Invalid argument. 'undefined', 'null', and 'function' can not be assigned.");
}
this.elements.push(element);
this.bubbleUp();
}
private bubbleUp(index = this.size - 1): void {
while (index > 0) {
const parentIndex = Math.floor((index - 1) / this._branchFactor);
if (this.compare(this.elements[parentIndex], this.elements[index]) < 0) {
this.swap(index, parentIndex);
index = parentIndex;
} else {
break;
}
}
}
private swap(index1: number, index2: number): void {
const temp = this.elements[index1];
this.elements[index1] = this.elements[index2];
this.elements[index2] = temp;
}
}This class is an abstract class. You can use this class for number, string, or anything else if you define the compare function.
Pop the highest priority node
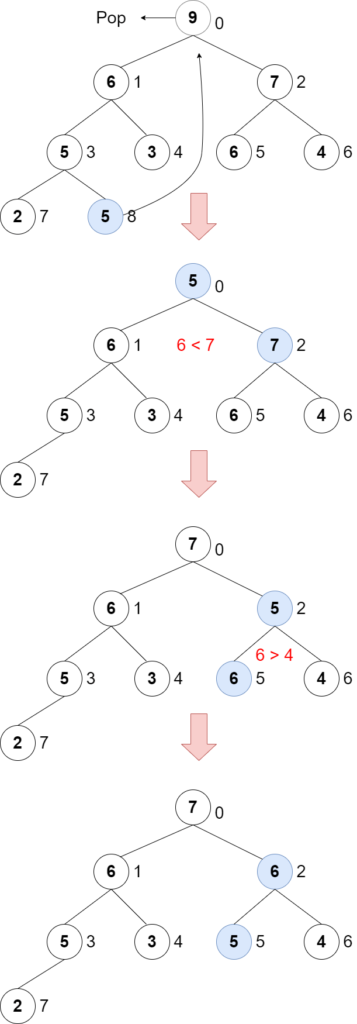
Let’s consider getting the highest priority node. If you pop the top node, the top node will be empty. It needs to be handled in the following way.
- Remove the top node
- Move the end node to the top node
- Compare the node with the child node that is the highest priority
- Swap the nodes
- Repeat step 2 – 4
It’s important to choose the highest priority node in the children to compare. Otherwise, the tree will violate the rule.
export abstract class DwayHeapBase<T> {
/**
* Remove the first element and return it if the heap is not empty.
*/
public pop(): T | undefined {
if (this.size < 2) {
return this.elements.shift();
}
// Must not delete the first element here
const firstElement = this.elements[0];
const lastElement = this.elements.pop();
this.elements[0] = lastElement!;
this.pushDown();
return firstElement;
}
private pushDown(index = 0): void {
const firstLeafIndex = Math.floor((this.size - 2) / this.branchFactor + 1);
const currentElement = this.elements[index];
let currentIndex = index;
while (currentIndex < firstLeafIndex) {
let smallestChildIndex = this.branchFactor * currentIndex + 1;
// If there is only one child, this.size is returned
const largestChildIndex = Math.min(this.branchFactor * currentIndex + this.branchFactor, this.size);
let highestPriorityElement = this.elements[smallestChildIndex];
let childIndex = smallestChildIndex;
for (let i = smallestChildIndex; i < largestChildIndex; i++) {
const compareResult = this.compare(highestPriorityElement, this.elements[i + 1]);
if (compareResult < 0) {
highestPriorityElement = this.elements[i + 1];
childIndex = i + 1;
}
}
if (this.compare(currentElement, highestPriorityElement) < 0) {
this.swap(currentIndex, childIndex);
currentIndex = childIndex;
} else {
break;
}
}
}
}DON’T remove the first element. If you remove it, the array’s length will change and not work.
In the pushDown method, firstLeafIndex is calculated because it’s not possible to go down further. That’s the bottom position.
Update a node
Let’s implement update logic. Firstly, the value needs to be searched from the array. If the array doesn’t contain the value, it can’t update it.
It depends on the value in which direction the node needs to go, top or bottom.
export abstract class DwayHeapBase<T> {
public update(oldValue: T, newValue: T): void {
const index = this.elements.findIndex((x) => this.equal(x, oldValue));
if (index < 0) {
throw Error(`oldValue not found: ${oldValue}`);
}
this.elements[index] = newValue;
const compareResult = this.compare(oldValue, newValue);
if (compareResult === -1) {
this.bubbleUp(index);
} else if (compareResult === 1) {
this.pushDown(index);
}
}
}The image is below.
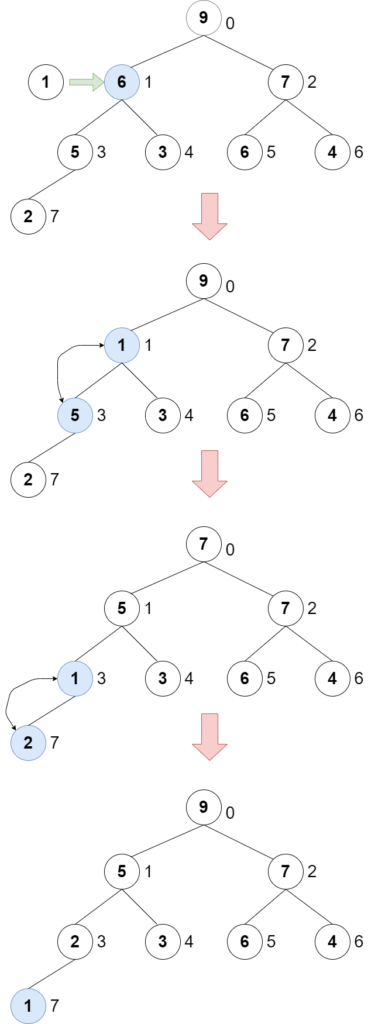
It takes a while to search the old value if the array is super big. This will be optimized later.
Remove a node
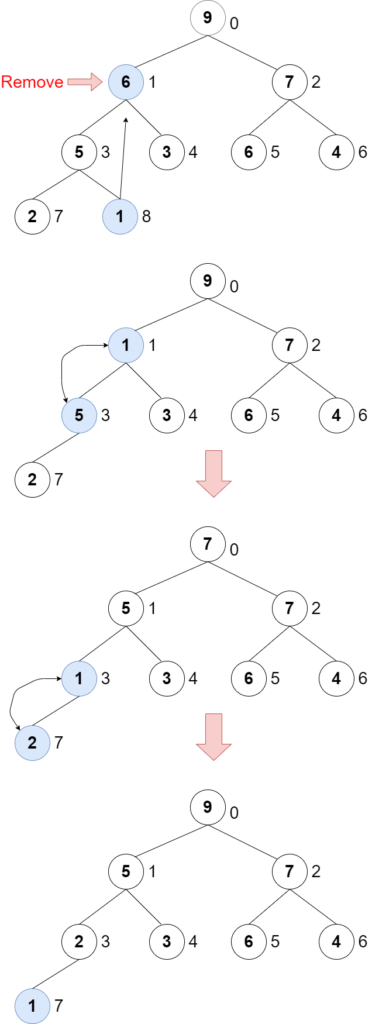
Removing a node is similar to pop. pop method removes the top node. This remove method can remove a middle node. The logic is the same as pop and update method.
export abstract class DwayHeapBase<T> {
public remove(element: T): void {
if (this.size === 0) {
throw ReferenceError("")
}
const index = this.elements.findIndex((x) => this.equal(x, element));
if (index < 0) {
throw ReferenceError(`element nod found: ${element}`);
}
this.elements[index] = this.elements.pop()!;
const compareResult = this.compare(element, this.elements[index])
if (compareResult === -1) {
this.bubbleUp(index);
} else if (compareResult === 1) {
this.pushDown(index);
}
}
}
Optimization of searching a node
It is not a nice approach to check one element by one element to search a node. The time increases linearly. Let’s use a hash table to improve this. If we use a hash table, the value can immediately be found.
For this reason, push method needs to be updated first.
We will put the index of the value when a new node is added. In addition to that, we can improve the logic.
It is not best to swap two nodes until the target node finds the desired place. If a new node is added, the new node is assigned to the swapped position every time but it’s enough if the node is assigned to the desired node at the end.
Instead, just copy the swapped node to the added node. The node duplicates during the process but the total number of processes decreases.
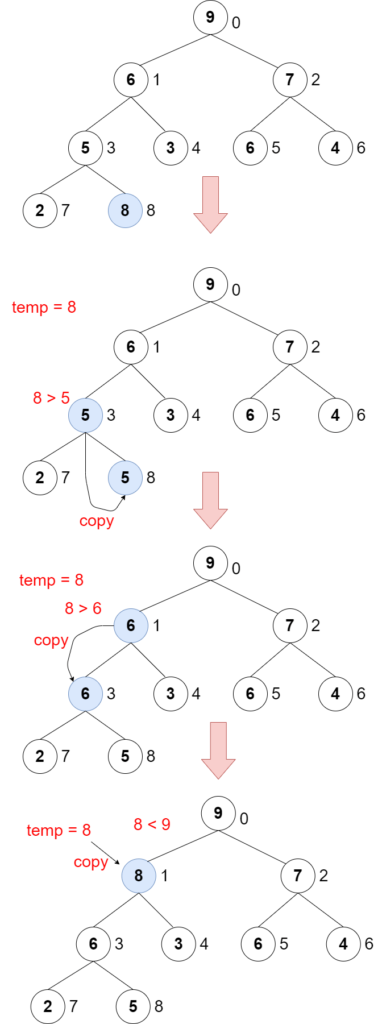
This is push method for optimized version.
export abstract class DwayHeapBaseOptimized<T> {
private positions = new Map<T, number[]>();
public push(element: T): void {
if (element === undefined || element === null || typeof element === "function") {
throw new TypeError("Invalid argument. 'undefined', 'null', and 'function' can not be assigned.");
}
this.setElementToPositions(element, this.size);
this.bubbleUp();
}
private bubbleUp(index = this.size - 1): void {
const currentElement = this.elements[index];
let currentIndex = index;
while (currentIndex > 0) {
const parentIndex = Math.floor((currentIndex - 1) / this._branchFactor);
if (this.compare(this.elements[parentIndex], currentElement) < 0) {
this.setElementToPositions(this.elements[parentIndex], currentIndex, parentIndex);
currentIndex = parentIndex;
} else {
break;
}
}
this.setElementToPositions(currentElement, currentIndex, index);
}
private setElementToPositions(element: T, index: number, oldIndex?: number): void {
const elementPositions = this.positions.get(element);
if (elementPositions === undefined) {
this.positions.set(element, [index]);
} else {
if (oldIndex !== undefined) {
const indexOfOldIndex = elementPositions.indexOf(oldIndex);
elementPositions.splice(indexOfOldIndex, 1);
}
elementPositions.push(index);
}
this.elements[index] = element;
}
}setElementToPositions method is used here to put the index. It stores the index and it is an array to address duplicates.
The positions variable can be used in remove method for example.
export abstract class DwayHeapBaseOptimized<T> {
public remove(element: T): void {
if (this.size === 0) {
throw ReferenceError("")
}
const indexes = this.positions.get(element);
if (indexes === undefined) {
throw ReferenceError(`element nod found: ${element}`);
}
const firstOccurrenceIndex = indexes[0];
if (firstOccurrenceIndex === this.size - 1) {
this.popElement(this.size - 1);
return;
}
if (indexes.length === 1) {
this.positions.delete(element);
} else {
indexes.shift();
}
const lastElement = this.popElement(this.size - 1);
this.setElementToPositions(lastElement, firstOccurrenceIndex);
const compareResult = this.compare(element, this.elements[firstOccurrenceIndex])
if (compareResult === -1) {
this.bubbleUp(firstOccurrenceIndex);
} else if (compareResult === 1) {
this.pushDown(firstOccurrenceIndex);
}
}
private popElement(index: number, isRemove = true): T {
const element = this.elements[index];
const indexes = this.positions.get(element)!;
if (indexes.length === 1) {
this.positions.delete(element);
} else if (indexes.length > 1) {
const indexToBeDeleted = indexes.indexOf(index);
if (indexToBeDeleted < 0) {
throw RangeError(`index was not found: ${index}`);
}
indexes.splice(indexToBeDeleted, 1);
}
if (isRemove) {
this.elements.splice(index, 1);
}
return element;
}
}Performance Comparison
I compared the performance with the following code.
function run3() {
const count = 1000000;
const heaps = [
new DwayHeapNumber(),
new DwayHeapNumberOptimized(),
];
for (const heap of heaps) {
console.time("total1")
console.time("push1")
for (let i = 0; i < count; i++) {
const random = Math.floor(Math.random() * count);
heap.push(random);
}
console.timeEnd("push1")
console.time("update1")
for (let i = 0; i < 1000; i++) {
const newValue = Math.floor(Math.random() * count);
const index = Math.floor(Math.random() * count);
heap.update(heap.peek(index)!, newValue);
}
console.timeEnd("update1")
console.time("remove1")
for (let i = 0; i < 200; i++) {
const index = Math.floor(Math.random() * 200 );
heap.remove(heap.peek(index)!);
}
console.timeEnd("remove1")
console.time("pop1")
while (heap.pop() !== undefined) { }
console.timeEnd("pop1")
console.timeEnd("total1")
console.log("-----------")
}
}
run3()I also check the book author’s code. The result is the following.
| Method | Normal | Optimized | Author |
|---|---|---|---|
| push1 | 97.065ms | 1.716s | 1.748s |
| update1 | 6.024s | 13.728ms | 12.501ms |
| remove1 | 5.738ms | 9.991ms | nothing |
| pop1 | 448.91ms | 15.030s | 13.687s |
| total1 | 6.588s | 16.772s | 15.458s |
Push for the optimized version is slower than normal because there are more processes in it.
However, it is much faster to update a node than the normal version. If the random generator generates the worst case many times, the difference will be bigger.
The used values are random, so the condition is different but it could be used as a report.
Related Articles
Check the following post too if you want to learn further data structure. Treap is tree + heap. So what you learned in this post is the base knowledge.
The following book is very thick. I will try to implement the algorithms explained in the book.
Advanced Algorithms and Data Structures




Comments